Binary Trees

Binary Tree

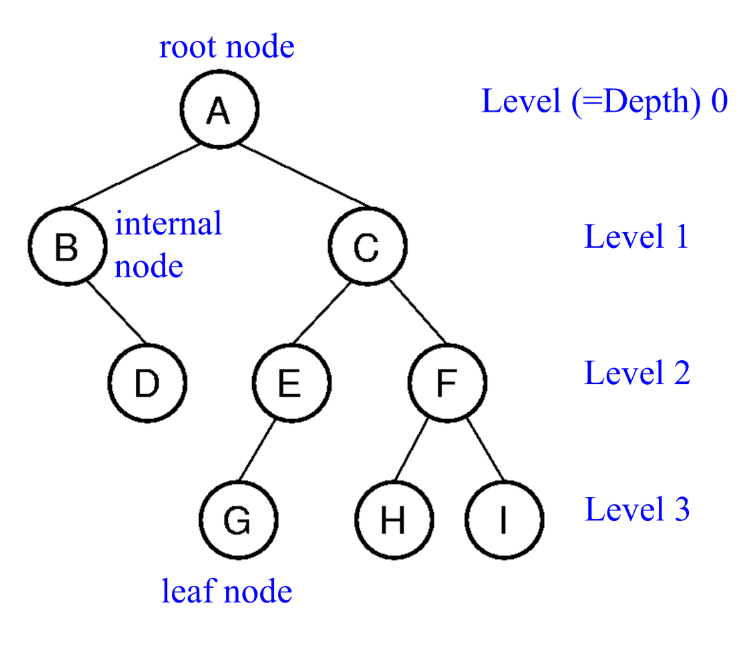
Full binary tree

각각의 node가 leaf(자식이 없는 노드)이거나 두 개의 자식을 가지고 있는 internal node인 tree.

Full binary tree

 

Complete binary tree

마지막 level을 제외한 모든 level이 완전히 차있어야(full) 한다.

가장 마지막 level은 모든 노드들이 왼쪽부터 채워져 있어야 한다.

Complete binary tree

 

Full Binary Tree Theorem

(1) non empty full binary tree의 leaves 수는 internal node의 개수보다 1개 더 많다.

Mathematical Induction을 이용하면 쉽게 증명이 가능하다.

 

위 theorem을 이용하면 non-empty tree에 대해서 null pointer의 개수가 tree의 node 개수보다 1개 더 많다는 것도 추론할 수 있다.

-> null pointer들을 leaf node로, 원래 node를 internal node로 보면 위의 Theorem을 적용할 수 있다.

non empty tree에 null pointer를 표시해 놓은 모습

 

 

Traversals

node를 방문하는 순서를 traversal이라고 한다.

 

Preorder traversal

자식 노드를 방문하기 전 각각의 노드를 방문

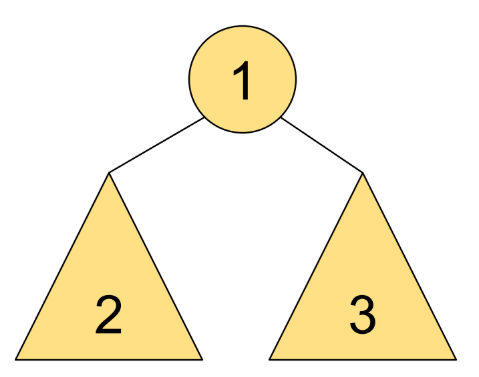
Postorder traversal

자식 노드를 방문한 후 각각의 노드를 방문

leaf들이 숫자이고 internal node가 연산자인 tree에서 postorder을 사용한다.

이런 수식이 있다면

이렇게 나타낼 수 있다

Inorder traversal

left subtree를 방문하고 그 다음 node를 방문. 그 후 right subtree를 방문

Binary Sort Tree에서 inorder traversal를 사용하면 순서에 맞게 정렬이 된다.

 

 

 

출처 : 서울대학교 컴퓨터공학부 강유 교수님 자료구조 수업